How Can We Help?
Geodesic Dome Frequencies Explained
Geodesic Dome Frequencies Explained
What is Dome Frequency?
When discussing geodesic domes, the frequency of a dome indicates how many times each of the sides of a triangulated base (face) is subdivided to create additional sections, aka struts. Those new points are, then, connected to divide the original triangle into smaller triangles.
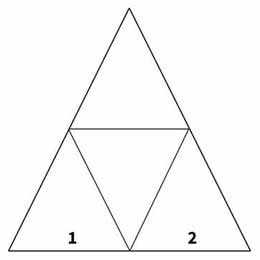
We can use the natural equator (triangle mid-point) to form a perfect hemisphere by dividing it in half.
In common terms, this same action is repeated throughout the entire dome structure as frequency. In dome science, when describing the harmonics of dome architecture, this repetition creates subtle frequency waves that generate certain energetic qualities within a dome’s structure.
An icosahedron is one of nature’s five platonic solids and is composed of 20-triangulated faces.
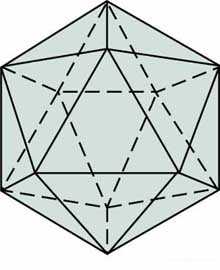
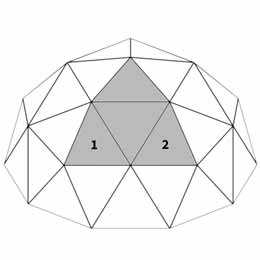
In a geodesic dome, each pentagon (5-sided, angled shape) represents the hub of the original icosahedron face. Removing one or more of the bottom sections of an icosahedron sphere is what creates a free-standing hemisphere.
Imagine geodesic dome frequency as having density. For example, we might start with a base figure of an icosahedron (20-sided face) and divide each edge within a triangulated face into 3 equal lengths. Those new points are connected to divide the original triangle into 9 smaller triangles. Since the original edges were divided into 3-parts, we call this a 3-frequency (3v) dome.
A geodesic dome’s frequency is commonly abbreviated as “v”. Thus, a 2-frequency dome is called 2v, 3-frequency is 3v, and so forth.
Example: By dividing each side of a triangle by 2, we achieve a 2v dome – dividing each side of a triangle by 3, gives us a 3v dome. This means that there are more struts within the same triangular base figure – the higher the frequency, the more struts there are – and, the more sphere-like the dome appears.
Why would you want to add more struts? Well, if this makes sense, as the size of the dome increases, more struts are necessary to add to the domes’ structural integrity.
How to determine Dome Frequency
You can determine the frequency of any dome by counting the number of struts between the centers of two pentagons (5-sided, angled plane). Again, the higher the frequency, the more curved or spherical it becomes. No matter the size, the higher the frequency, the stronger the dome structure becomes – increasing the number of struts increases its structural integrity.
The natural hemisphere of an ODD frequency dome lands not on the true equator, but at either 3/8ths or 5/8ths. Pacific Domes uses the 5/8ths measurement to maximize a dome’s height.
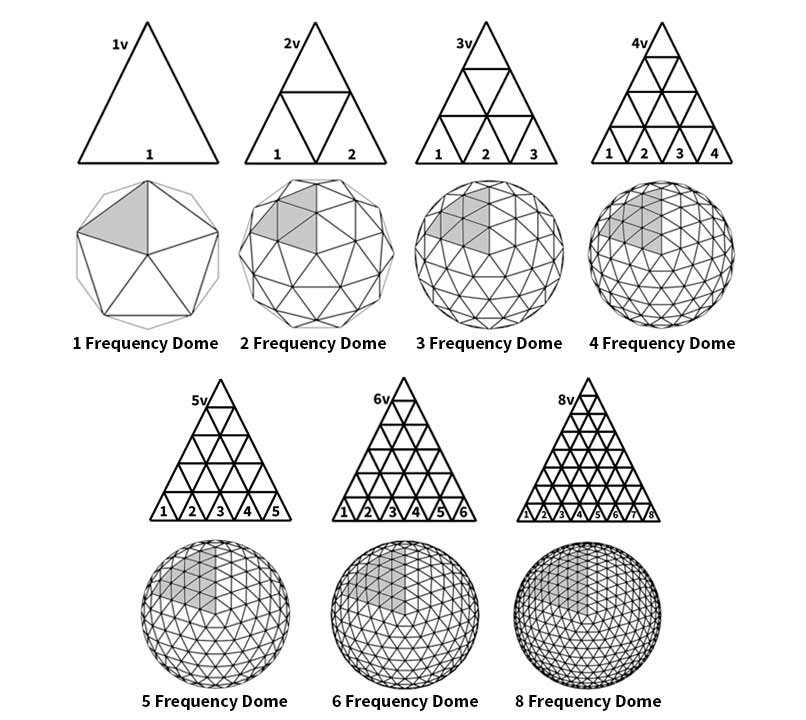
A 16-ft. dome is a 2v hemisphere. The 16-ft. tall Pacific Dome is a 2v with an added row for height.
The 20-ft. domes and 24-ft. domes are 3v domes.
A 30-ft. Pacific Dome is a 4v dome. and a 36-ft. dome is a 5v dome.
Pacific Domes 44-ft. to 90-ft. domes are 6v domes.
Lastly, Pacific Domes 120-ft. dome is an 8v frequency hemisphere dome.
R. Buckminster Fuller, father of the modern geodesic dome, spent many years observing and working with the harmonic geometry of nature. He evolved a monolithic structure based on the structural integrity of triangulation found everywhere in nature. Marshall Lefferts in his book, “Cosmometry”, explores how domes have proven time and again to be the strongest structure known to man in regions of the planet prone to nature’s extremes, such as high winds and snow storms, hurricanes, tornadoes and earthquakes.
Geodesic Dome Frequencies Explained (video)!
Everything in nature is born from one of the Platonic solids: Named after the ancient Greek philosopher Plato, platonic solids are geometric shapes where the same number of sides meet at each vertex with the same length and angle to create equal forces. They are the only stable structures found in nature. The five platonic solids that meet these criteria are: The tetrahedron which is associated with the element of fire, The cube, which is earth The octahedron, which is air The dodecahedron, which is the cosmos, and lastly, and most complex is the icosahedron, a 20-sided spherical shape which is associated with the element of water.
